
Variational autoencoders attempt to encode high dimensional data such as images into smaller, normally distributed latent vectors. These representations can then decoded and reconstructed. This article describes my VAE experiments and results.
An autoencoder is essentially a compression algorithm - the network attempts to reconstruct input data without losing information. The "bottleneck" of the model is the latent space - the compressed representation. The decoding part of the network can reconstruct data using this latent vector.

Before moving to the more complex variational autoencoder, I have implemented variations of regular autoencoders. In this section I will discuss the models briefly, as well as issues I faced in the hope that other beginners in the field may find them useful.
The model consists of two networks - the encoder and decoder.
The encoder is similar to an image classification network, and uses convolutional layers to reduce the dimensionality of the input data. Instead of an output label, we are interested in a latent representation. I have used between 3 and 5 convolutional layers in my experiments, with kernel sizes of 3 and 5 and strides of 1 and 2 for most layers.
The decoder can be imagined as an inversed encoder network, and uses convolutional transposition layers as opposed to regular convolutions. This has the affect of scaling the smaller latent vector into a larger output image. The following illustration is very helpful in visualizing a single filter in a transposition layer. All credit for this illustration goes to vdumoulin.
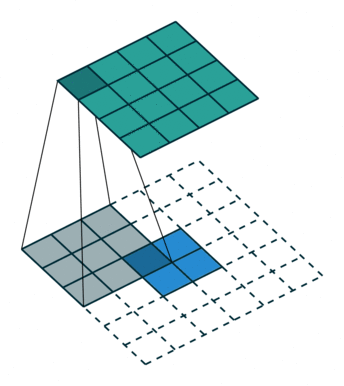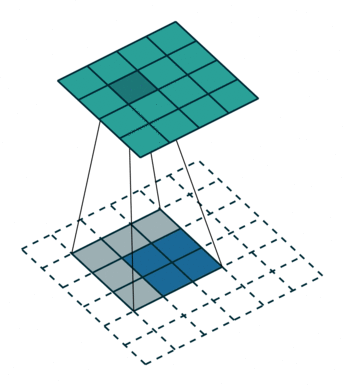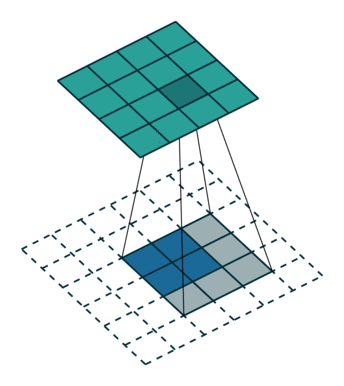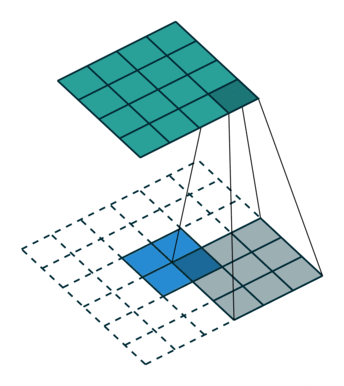
My initial attempts used the mean squared error as the loss function, and a small dataset of ~150 augmented images. After training I achieved acceptable, though quite blurry results. I used a latent size of 128 for this attempt.

Due to the blurriness of the result, I decided to investigate the effect of the latent size - keeping all other factors constant. I tested latent sizes of 64, 128, 256, 512 and 1024. All results are after 30 epochs of training.

The best results were achieved with latent sizes between 128 and 512 on this dataset. Interestingly, a latent size of 1024 proved a significant reduction in quality. I suspect this could be prevented with more training or using a better dataset and model, but it would also be prone to overfitting.
After further architecture tweaks, hyperparameter tuning and longer training sessions I achieved better results on grayscale images as seen below.

In a regular autoencoder there are no constraints on the distribution of latent vectors. This means that the model will often separate examples in a non-continuous fashion. In other words, reconstructing latent vectors which are not explicitly encoded from an image in the dataset will yield poor results with no meaningful spatial structure. The below figure is an example of some generated images which illustrates this problem more clearly.

The largest change in a variational autoencoder is the enforcement of a gaussian distribution in the latent space. In order to achieve this, the Kullback-Leibler divergence (KL divergence) is incorporated in the loss function of the network. KL divergence describes the difference between one probability distribution and another - in this case the difference between the latent distribution and a normal distribution. In order to incorporate this error, the encoder estimates two vectors instead of one - one of means, and one of standard deviations.
To test the variational autoencoder, I first trained a network repeatedly on a single (augmented) image. The generated results closely match what you would expect. Note that the bottom images are not direct reconstructions, but random samples of the latent space.

Because each image can be encoded as a latent vector, you can interpolate between vectors and expect the generated images to keep some spatial consistency. If each step between the two (real) images also look real, the generative network will be quite powerful indeed. My initial attempts used small datasets and were therefore unsuccessful. The example below illustrates some weak spatial consistency (particularly around the ears), but intermediate images are still difficult to recognize.

Although cats are interesting, my dataset proved too small to achieve acceptable results. I decided to employ the mnist dataset using the same model, which allowed the model to construct more meaningful latent spaces. Notice the consistency of lines during transitions. Each step remains spatially consistent. Also note that this particular model was not concerned with the label (the actual number) each image represents.

Autoencoders attempt to reconstruct data from a compressed latent representation. Variational autoencoders have the additional requirement of encoding data in a normally distributed latent space.
My model has proved fair reconstruction abilities with the small cat dataset, but struggles with previously unseen latent vectors. Using the mnist dataset, results are overall decent and maintain spatial coherency.
This project is open source and is available on my GitHub.