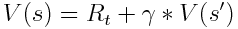
PPO is a powerful reinforcement learning algorithm which attempts to estimate the policy directly based on running estimates of action advantages. This article describes my intuitions behind how PPO works, as well as my results in training a biped to walk using proximal policy optimization with objective clipping.
In traditional Q learning, the actor attempts to estimate the function Q(s,a) which maps every action a to some reward r for every state s. Intuitively, this is enough to behave correctly in the environment. Given an optimal Q function, choosing the action a for which r is highest will be equivalent to an optimal policy pi(s) = a .
In a large or continuous action space, this type of deep Q learning is not possible. Proximal policy optimization, however, does not estimate the Q function. Instead, it attempts to estimate the policy directly based on an estimated value function V(s).
In order to improve the policy, we need some kind of measure to see how the policy is doing. The critic is responsible for this, by estimating the value function V(s). This function describes the expected value of any state, if we were to follow the current policy. We can estimate this function using a deep neural network. The estimated expected reward can be formulated as
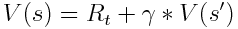
where gamma is a falloff rate between 0 and 1 which indicates the importance of temporal distance in rewards. To illustrate this, imagine a collectible in a game with a reward of 10 points. Given a gamma falloff rate of 0.95, the reward 5 units of time in the future would be
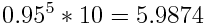
The actor would therefore prefer to pick up the collectible now for an immediate reward of 10, but the future rewards is still taken into account - especially if it significantly greater.
An intuitive way to estimate the improvement of the policy would be to compare the total episode reward with the estimation. This would indeed indicate if the policy is converging, but suffers from the credit assignment problem. If the actor did something particularly well in a bad situation, it may still get punished if the overall reward is low. To avoid this, the advantage of each transition is used instead. The function tells us how much better an action in any given state was than the expectation of the critic. The advantage is calculated as follows:
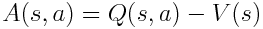
Now we have a powerful measure to train the policy. Actions with a high advantage were surprisingly good and should therefore be made more likely in the future, whereas actions with a negative advantage must be discouraged.

Figure: suboptimal walking policy after 500 episodes of training
In many reinforcement learning problems the action space is continuous. This means that a softmax mapping to action probabilities is not possible. Instead, we can map each state to a stochastic probability distribution. A gaussian distribution can be described with just two numbers - sigma and mu - as illustrated below.
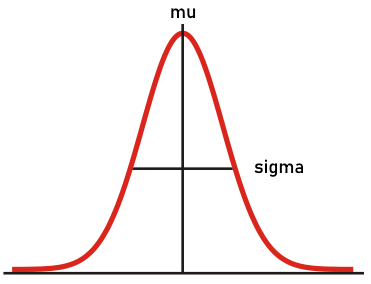
Figure: the policy network should estimate two vectors, which together describe the stochastic policy.
PPO is a hill climbing algorithm which attempts to climb to a local maxima in parameter space with respect to the reward in the environment. Since the gradient is directed by an estimated value function which may not be correct, the actor is prone to policy collapse - especially in more complex environments. One can imagine this as falling off a cliff, unable to get up again.
PPO introduces two key ways to avoid these problems: PPO-penalty and PPO-clip. Penalty indicates an addition to the loss function. By punishing the KL divergence from the previous policy, we can prevent small changes in parameter space triggering large changes in the policy.
Another way to prevent collapse is clipping. This method attempts to clip terms in the objective function to prevent too large deviations. Given a policy loss function of
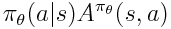
we incorporate a clipping based on the difference between the old and new policy:
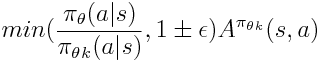
The min function indicates a clipping based on the difference between the new and old policies. The clipping prevents excessive divergence from the old policy. See this OpenAI article for a great explanation on how clipping works in PPO.
I have tested my implementation of PPO in the lunar lander and bipedal walking OpenAI environments.
The continuous lunar lander task was solved after 5300 episodes of training with a mean score of 224. The task did not experience performance collapse, and training seemed quite stable overall.
Figure: lunar lander solved after 5300 episodes of training
I was unable to solve this environment. The actor successfully learned suboptimal walking strategies yielding positive reward, but was unable to improve further due to a high frequency of early falls. I suspect this is due to some weaknesses in my advantage estimations, which make the objective function misaligned with the goal of a high mean reward.

Figure: adequate walking policy after 1000 episodes of training. This actor still experienced a near 50% fall rate in the beginning of episodes.
This project is open source, and is available on my GitHub.